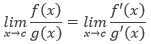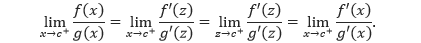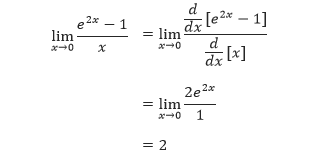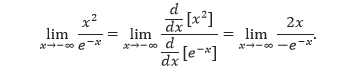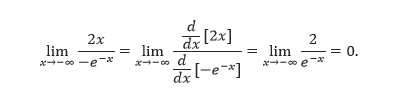Penerapan Turunan Fungsi

Penerapan Turunan Fungsi 

Definisi Turunan 

DEFINISI Turunan suatu fungsi f pada bilangan a, dinotasikan dengan f’(a), adalah 

Aturan-Aturan Turunan

Turunan Fungsi Trigonometri

CONTOH PENERAPAN FUNGSI TURUNAN:

1.

Sebuah kotak berbentuk prisma tanpa tutup mempunyai alas persegi. Jika volume kotak tersebut 13.500 cm³, luas permukaan minimum kotak yang dapat dibuat adalah . . ..

A.    2.100 cm²

B.    2.400 cm²

C.    2.700 cm²

D.    3.200 cm²

E.    3.600 cm²

Pembahasan:

2. 

Reaksi terhadap sebuah obat insektisida setelah t jam disemprotkan pada tanaman dapat dinyatakan sebagai bilangan tak negatif yang sama dengan R(t) = 12t² – t³. Reaksi maksimum dicapai pada saat t = . . . .

A.       2 jam

B.       4 jam

C.       6 jam

D.       8 jam

E.       12 jam

     Jawaban: D

R(t) = 12t² – t³

Reaksi mencapai stasioner pada saat R¢(t) = 0

           R'(t)   = 0

    24t – 3t²   = 0

      3t(8 – t)   = 0

       t = 0 atau t = 8

Menguji t yang menyebabkan reaksi maksimum.

R''(t) = 24 – 6t

R''(0)     = 24    (minimum)

R''(8)     = -24   (maksimum)

Jadi, obat tersebut akan mencapai reaksi maksimum pada saat   t = 8 jam.

3. 

Coba tentukan nilai maksimum dari fungsi f (x) = 3x (x2 – 12)

Jawab :

Nilai maksimal yang didapatkan ketika f’ (x) = 0

Uraikan kemudian turunkan di fungsi berikut :

f (x) = 3x (x2 – 12)

f (x) = 3x3 – 36x

f’ (x) = 9x2 – 36 = 0

9x2 = 36

X2 = 4

X = akar dari 4 = +- 2

Untuk x = +2

f (x) = 3x3 – 36x = 3 (2)3 – 36 (2) = 24 – 72 = -48

Untuk x = -2

F (x) = 3x3 – 36x = 3 (-2)3 – 36 (-2) = -24 + 72 = 48

Maka nilai minimum adalah -48 dan nilai maksimum adalah 48.

sekian materi penerapan turunan fungsi saya sampaikan, semoga dapat bermanfaat. berikan komentar sebagai feedback saya. Terima Kasih telah membaca

Bentuk Tak Tentu dan Aturan L'Hospital

Aturan L'Hopital 

    Aturan L’Hôpital menyatakan bahwa dalam kondisi tertentu, limit dari pembagian f(x)/g(x) dapat ditentukan dengan menggunakan limit pembagian dari turunan-turunannya, yaitu

    Untuk membuktikan teorema ini, digunakan Teorema Nilai Rata-rata yang Diperluas, seperti berikut.

    Setelah membuktikan Teorema Nilai Rata-rata yang Diperluas, sekarang perhatikan Teorema L’Hôpital berikut.

ATURAN L’HÔPITAL
Misalkan f dan g adalah fungsi-fungsi yang memiliki turunan pada interval terbuka (a, b) yang memuat c, kecual pada c itu sendiri. Anggap g(x) ≠ 0 untuk setiap x di (a, b), kecuali pada c itu sendiri. Jika limit dari f(x)/g(x) untuk x mendekati c menghasilkan bentuk tidak tentu 0/0, maka

apabila limit di ruas kanan ada (atau tak hingga). Hasil ini juga dapat diterapkan jika limit f(x)/g(x) untuk x mendekati c menghasilkan bentuk-bentuk tak tentu ∞/∞, (–∞)/∞, ∞/(–∞), dan (–∞)/(–∞).

Akhirnya, dengan memisalkan x mendekati c dari kanan, x → c+, didapatkan z → c+ karena c < z < x, dan

CONTOH:

1. Bentuk Tak Tentu 0/0

Tentukan nilai limit dari (e2x – 1)/x untuk x mendekati 0.

Pembahasan Karena dengan menggunakan substitusi langsung menghasilkan bentuk tak tentu 0/0,

sehingga dapat diterapkan Aturan L’Hôpital, seperti yang ditunjukkan di bawah ini.

2. Penerapan Aturan L’Hôpital Lebih dari Satu Kali

Tentukan limit x2/e–x untuk x mendekati negatif tak hingga.

Pembahasan Karena dengan substitusi langsung akan menghasilkan bentuk tak tentu ∞/∞, maka gunakan Aturan L’Hôpital.

Limit ini masih menghasilkan bentuk tak tentu (–∞)/(–∞), sehingga Aturan L’Hôpital dapat diterapkan kembali.

 

Bentuk Tak Tentu

Bentuk Tak Tentu

Bentuk tak tentu adalah bentuk yang nilainya sembarang, misalnya:

 Untuk membuktikan bahwa nilai  merupakan bentuk tak tentu. Maka pertama, misalkan hasilnya adakah x, dengan x adalah anggota bilangan real.

Dari betuk terakhir, kita harus mencari bilangan x sehingga jika dikalikan dengan nol hasilnya nol. Dan jawabannya adalah semua bilangan. Oleh karena itu, bentuk  merupakan bentuk tak tentu karena jawabannya banyak.

 

Begitu pula dengan  memiliki jawaban yang banyak sehingga bentuk- bentuk tersebut juga dikatakan bentuk tak tentu.

 

Berikut dua teorema penting untuk mempelajari limit-limit tak tentu :

1. Bentuk tak tentu 0 :

                

Cara penyelesaian : Ubahlah bentuk f(x)/g(x) sehingga sifat-sifat limit fungsi dapat digunakan. Cara yang dapat dicoba adalah menguraikan pembilang dan penyebut, menggunakan rumus trigonometri, merasionalkan bentuk pecahannya, dan sebagainya.

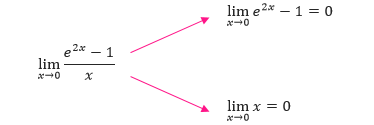
Perhitungan limit bentuk tak tentu 0/0 diberikan dalam contoh berikut :

Contoh Bentuk 0/0 :

2. Bentuk tak tentu  ∞/∞ :

Cara penyelesaian : Ubahlah bentuk f(x)/g(x) sehingga sifat-sifat limit fungsi dapat digunakan. Cara yang dapat digunakan adalah merasionalkan bentuk pecahannya, memunculkan bentuk 1/x pangkat n, n bilangan asli, dan sebagainya.

Perhitungan limit bentuk tak tentu ∞/∞ diberikan dalam contoh berikut :

Contoh Bentuk ∞/∞ :

 

3. Bentuk tak tentu 0.∞ :

Contoh Bentuk tak tentu 0.∞ :

4. Bentuk Tak Tentu ∞ – ∞ :

Contoh Bentuk   ∞ – ∞ :

sekian dari materi tak tentu, semoga bermantaat. Terima Kasih telah membaca

Aturan Rantai dan Turunan Implisit

Aturan Rantai dan Turunan Implisit

Aturan Rantai

Teorema Aturan Rantai

Misalkan f(u) terturunkan di u=g(x) dan g(x) terturunkan di x ,maka fog (x) terturunkan di x

 

fog’(x)=f’(g(x)). g’(x)

 

Bentuk Fungsi Yang Diturunkan Dengan Aturan Rantai

1.    1.   

f(x)ⁿ

2.     2.  Sin(f(x))

3.      3. Sinⁿ(f(x))

Contoh Soal dan Pembahasan Aturan Rantai

Contoh Soal 1

y= (1+x)¹⁵  → f(x)ⁿ

u= 1 +x

y= U¹⁵

       =.

       = 15 u⁴ ₍₁₎

       = 15 u¹⁴

       = 15 (1+x)¹⁴

Contoh Soal 2

y= sin (x²) = Sin (f(x))

u= x²

y = sin u

            = .

             = cos (u) . (2x)

             = 2x cos (u)

             = 2x cos (x²)

 

Turunan Implisit

·         Fungsi Eksplisit =

y = f(x)

·         Fugsi Implisit

f(x.y) = c

Cara Menurunkan

1.      Turunkan kedua ruas terhadap x

2.      Gunakan aturn rantai

3.      Tentukan

Contoh Soal

=

Diturunkan =

(1)(y²) + (x)(2y)(

Y² + 2xy =1

       2xy =1 -y²

                      =