Aturan L'Hopital
Setelah membuktikan Teorema Nilai Rata-rata yang Diperluas, sekarang perhatikan Teorema L’Hôpital berikut.
ATURAN L’HÔPITAL
Misalkan f dan g adalah fungsi-fungsi yang memiliki turunan pada interval terbuka (a, b) yang memuat c, kecual pada c itu sendiri. Anggap g(x) ≠ 0 untuk setiap x di (a, b), kecuali pada c itu sendiri. Jika limit dari f(x)/g(x) untuk x mendekati c menghasilkan bentuk tidak tentu 0/0, maka
apabila limit di ruas kanan ada (atau tak hingga). Hasil ini juga dapat diterapkan jika limit f(x)/g(x) untuk x mendekati c menghasilkan bentuk-bentuk tak tentu ∞/∞, (–∞)/∞, ∞/(–∞), dan (–∞)/(–∞).
Akhirnya, dengan memisalkan x mendekati c dari kanan, x → c+, didapatkan z → c+ karena c < z < x, dan
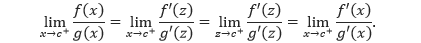
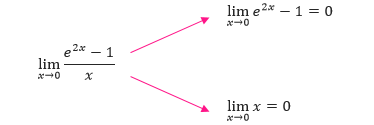
Tentukan nilai limit dari (e2x – 1)/x untuk x mendekati 0.
Pembahasan Karena dengan menggunakan substitusi langsung menghasilkan bentuk tak tentu 0/0,
sehingga dapat diterapkan Aturan L’Hôpital, seperti yang ditunjukkan di bawah ini.
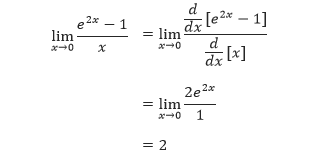
Tentukan limit x2/e–x untuk x mendekati negatif tak hingga.
Pembahasan Karena dengan substitusi langsung akan menghasilkan bentuk tak tentu ∞/∞, maka gunakan Aturan L’Hôpital.
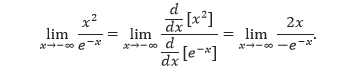
Limit ini masih menghasilkan bentuk tak tentu (–∞)/(–∞), sehingga Aturan L’Hôpital dapat diterapkan kembali.
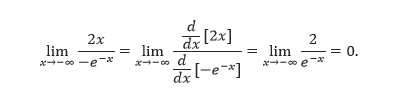



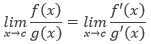
No comments:
Post a Comment